Let’s start with Ayanokoji’s story!

He quietly sits in class 1-D, observing. He doesn’t ask questions, doesn’t seek attention, yet every move he takes is precise.You may have observed he doesn’t just act at random though he is learns, refine his strategies, and adapt to his environment.

Now, let’s dive into RL!

Before we start exploring, let’s understand what an Agent and an Environment is!

Agent

The agent is the learner or decision-maker. It interacts with the environment, takes actions, and learns from the feedback (rewards/penalties). The interaction is through trial and error while performing actions.

Ayanokoji, analyzing his classmates and making strategic moves.

Environment

The environment is everything the agent interacts with. It provides states, receives the agent’s actions, and gives rewards as feedback.

The Advanced Nurturing High School, full of unpredictable students and hidden rules (for Ayanokoji).

One important note here is, each action executed is without any supervision because that’s how we as human learn (through interaction).

RL is just a computational approach of learning from actions.

---

The RL Framework!

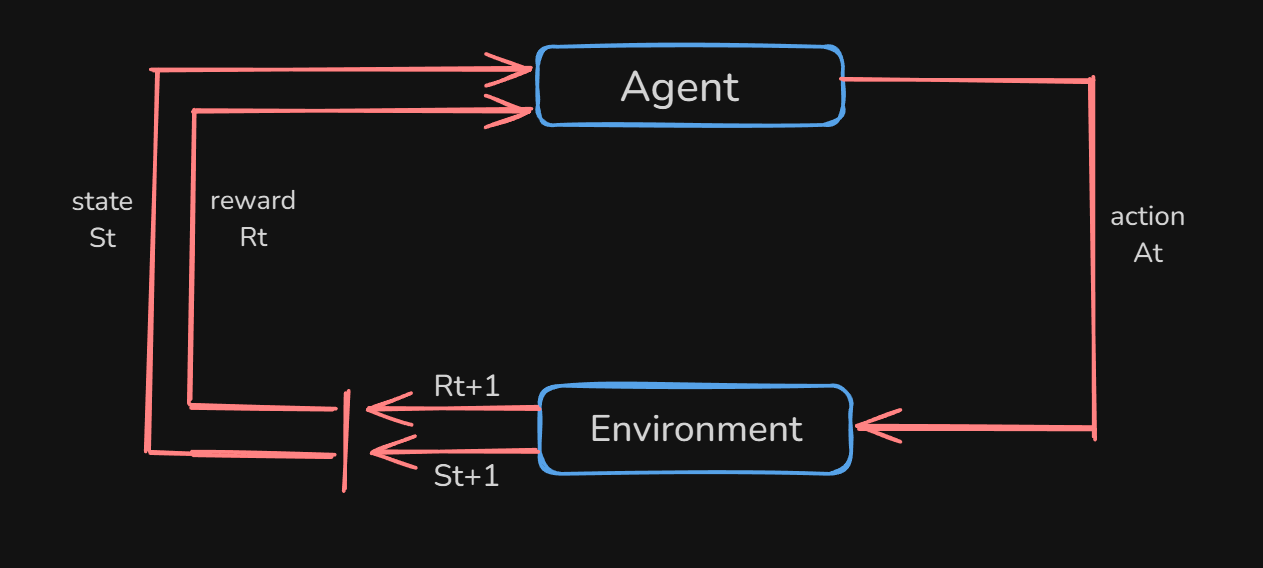
RL Process.

The RL Process is a loop of state, action, reward and next state.

RL models decision making in an interactive environment where an agent learns to take actions to maximize cumulative rewards.

The process follows Markov Decision Process (MDP), which consists of:

• State Space (S): The set of all possible states $s_t$ that can be in.
• Action Space (A): The set of all possible actions $a_t$ that can take.
• Transition Dynamics (P(s’|s, a)): The probability of moving to a new state s’ given the current state ‘s’ and action ‘a’.
• Reward Function (R(s, a)): A function that gives a scalar reward $r_t$ when the agent takes an action $a_t$ in state $s_t$

We will look into more RL terminologies:

• states, observations, action spaces
• policies
• trajectories
• different formulations of return
• Exploration and Exploitation Trade-off

States, Observation and Action Spaces

Imagine Ayanokoji in Classroom of the Elites. He always operates with perfect awareness of situations, analyzing every variable. If he knows everything about a scenario—his classmates’ intentions, hidden motives, and all external factors—that’s a state (complete information).

But most students don’t see the full picture. They only perceive what’s right in front of them—fragments of the truth. That’s an observation (partial information).

Fully vs. Partially Observed Environments

• Fully Observed: If Ayanokoji has access to all relevant data, he can make perfect decisions.
• Partially Observed: If he lacks key details (e.g., another class’s secret plan), he must strategize under uncertainty—just like RL agents in real-world applications.

So much like Ayanokoji, RL agents must decide whether they have all the facts or just a piece of the puzzle—and act accordingly.

The set of all the valid actions in a given environment is often called the action space. There are two types of action spaces, Discrete and Continuous.

Discrete action spaces are where only a finite number of moves are available to the agent.

In continuous action spaces, the agent fine-tune every move like a robot adjusting its joints. In robotics, actions aren’t just “move left” or “move right”—they involve continuous adjustments in angles and forces.

Policies

A policy is a rule used by an agent to decide what actions to take.

In Classroom of the Elite, Ayanokoji never acts randomly. Every decision follows a policy which is ****a rule that tells him what action to take in a given situation.

Imagine Ayanokoji is in a situation (let’s call it state $s_t$) The policy is like his mindset, deciding what action $a_t$ he should take:

$$Action = Policy(State)$$

A policy can be deterministic or stochastic.

Deterministic Policy

If Ayanokoji always picks the same action for a given situation, his policy is deterministic.

$$a_t = \mu(s_t)$$

👉 This just means: “In state $s_t$, take action $a_t$ with 100% certainty.”

Let’s say, if someone challenges Ayanokoji directly, he always acts calmly and stays unreadable i.e. the actions are deterministic.

Stochastic Policy

If Ayanokoji sometimes picks different actions in the same situation, his policy is stochastic.

$$a_t \sim \pi(\cdot \mid s_t)$$

👉 This means: “In state $s_t$, randomly choose an action $a_t$ based on some probability.”

When dealing with Kushida, Ayanokoji sometimes ignores her, sometimes manipulates her, and sometimes sets traps—all in the same situation. His decision is randomized but controlled, keeping opponents guessing.

Parameterized Policies In Deep RL, policies aren’t fixed they can learn and improve

over time! This is where parameters (like θ, which represent things like weights, biases) come in.

so, we now add a parameter θ that allows the policy to change as the agent learns.

We can think of θ as Ayanokoji’s experience level. The more he learns about his classmates, the better he tweaks his decision-making process.

Trajectories

A trajectory is a sequence of states and actions over time, like a story unfolding. For Ayanokoji, think of this as his journey in Classroom of the Elite. Every decision he makes (an action) affects the state of the world (class dynamics, rival reactions, etc.), forming a trajectory.

$$\tau = (s_0, a_0, s_1, a_1, . . . )$$

1. Starting point : The First State $(s_0)$

• The first state of the world is not chosen by the agent but sampled from a start-state distribution (ρ0​).
• Let’s say Ayanokoji didn’t choose to be in Class 1-D; he was placed there randomly, much like how an RL agent starts in a random initial state.

$$s_0 \sim \rho_0(\cdot)$$

1. State Transitions: How the World Evolves

• The environment follows rules (the “laws of the world”). These rules determine how the next state $s_{t+1}$ evolves based on the current state $s_t$ and action $a_t$
• This can be deterministic or stochastic

→ Deterministic (fixed outcome)

$$s_{t+1} = f(s_t, a_t)$$

→ Stochastic (random outcome)

$$s_{t+1} \sim P(\cdot \mid s_t, a_t)$$

We’ve discussed about fixed and random policies above.

Reward Functions

In RL, the reward function R defines how much benefit an agent gets from taking an action in a given state:

$$r_t = R(s_t, a_t, s_{t+1})$$

Accumulating Rewards over Time!

Ayanokoji is strategic, he doesn’t just focus on immediate gains but thinks long-term. RL agents also maximize cumulative reward (called return $R(\tau)$)

Finite-Horizon Undiscounted Return

If Ayanokoji is given a fixed time window (say, one semester), he sums up all rewards within that time:

$$R(\tau) = \sum_{t=0}^{T} r_t$$

This is useful when there’s a clear ending, like an exam or a competition.

Infinite-Horizon Discounted Return

What if the game never ends? Ayanokoji plays the long game, carefully planning years ahead. But future rewards matter less than immediate ones.

RL models this with a discount factor $\gamma \in (0,1)$ making near-term rewards more valuable:

$$R(\tau) = \sum_{t=0}^{\infty} \gamma^t r_t$$

Here, you may ask WHY DISCOUNT?

• “Cash now is better than cash later”—a win today is more certain than a possible win in the future.
• Mathematical stability—without discounting, the sum might not converge.

If Ayanokoji can manipulate someone now to make them an ally later, he’ll consider whether the future benefit is worth it. He won’t spend too much effort on uncertain long-term gains if he has better short-term opportunities.

Exploration and Exploitation: A Trade-off

We all know Ayanokoji is master strategist. He doesn’t blindly take actions—he carefully balances between learning about people (exploration) and using what he knows to win (exploitation).

In RL, this is known as the exploration-exploitation tradeoff. Let’s break it down.

The Trade-off Intuition

• Exploration (Try new things)

  → Gathering information about the environment, even if it doesn’t immediately maximize rewards.

• Exploitation (Use what you know)

  → Taking actions that already seem best based on known rewards.

Let’s understand this better:

If Ayanokoji immediately started manipulating people, he might miss hidden opportunities or underestimate opponents.

OR if he only kept gathering information forever, he’d never act and wouldn’t get real results.

Key trade-off: When should he gather more data vs. use what he already knows to win?

We need to balance how much we explore the environment and how much we exploit what we know about the environment.

Hope you enjoyed this (pretty much Ayanokoji story lol). I’ll come up with value functions, approaches to solving RL problems, and implementations (yes, we’ll train our RL agent) in next blog (coming soon). siuuuuuu!!